Approach Accuracy of Professional Golfers on the PGA Tour

Project description: This project was done as a part of the course CS-E5710 - Bayesian Data Analysis D. The project involved choosing a data set and then performing a whole analysis according to all the parts of Bayesian workflow. We decided to study the approach accuracy of professional golfers on the PGA tour. The intuition suggests that the farther the player starts from the hole, the more difficult it is to get close to it.

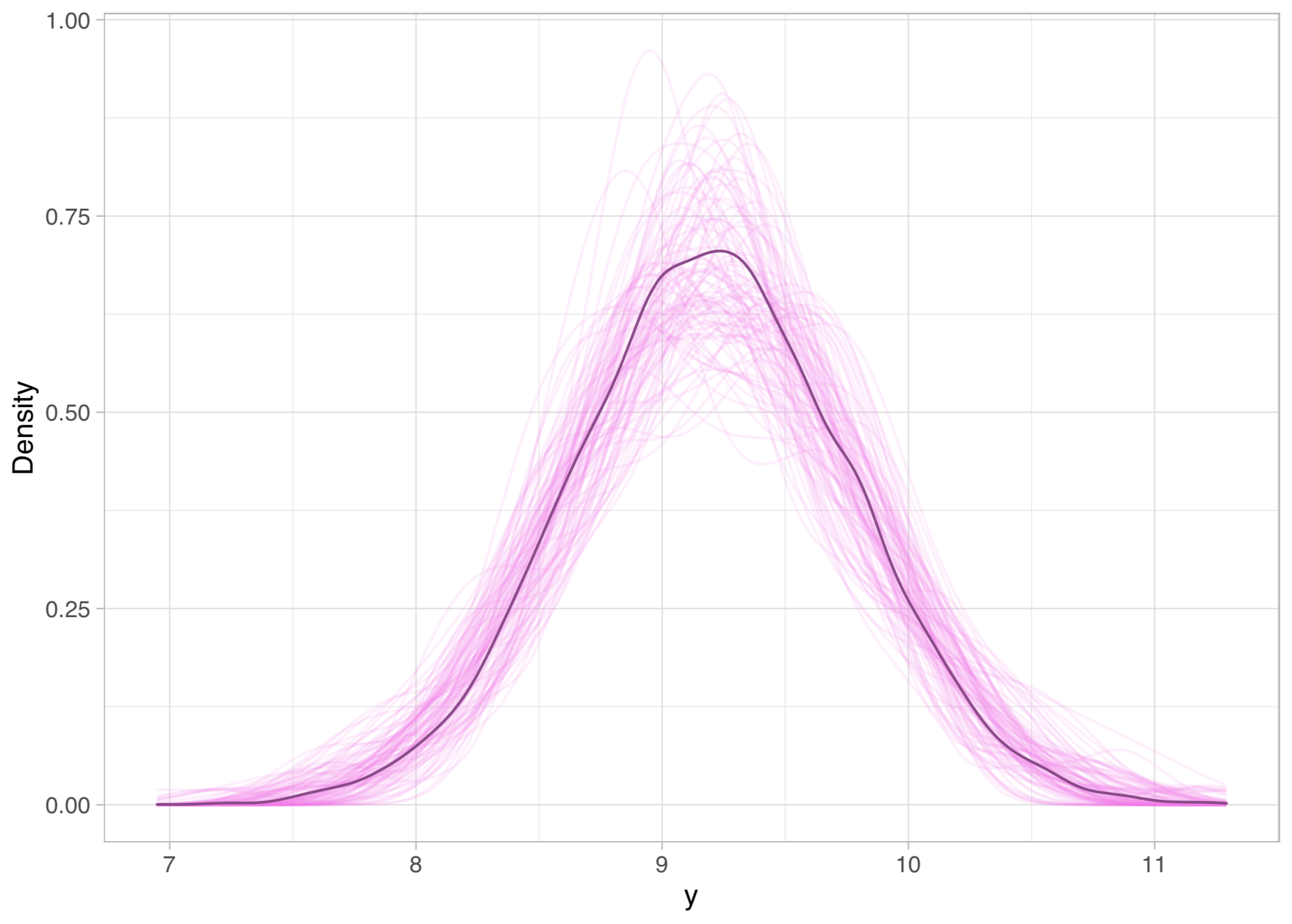
The dependency between the initial distance and the final distance from the hole is not very well understood - the functional dependency might be, for example, linear, quadratic, or any higher-order polynomial. Instead of trying to approximate a point estimate of the final distance, such as the expected final distance given the initial distance, we wanted to model the posterior predictive distribution for every possible initial distance. In other words, we wanted to be able to simulate golf shots from every potential initial distance from the hole.

Results: To meet the objective of our project, building a model that is applicable for predicting the distribution at arbitrary initial distances, we constructed a pooled model. This pooled model - Cubic Mean & SD - has pooled parameters for both the mean and the standard deviation, and that is what allows predicting the distributions of arbitrary initial distances. The goal of the project was met, and we were able to simulate a distribution of golf shots during one year for one player from an arbitrary initial distance.